[그리디알고리즘] 집합 커버 문제 / 강의실 배정 문제

그리디 알고리즘

5. 집합 커버 문제

n개의 원소를 가진 집합이 있고 이 집합의 부분 집합을 원소로 하는 집합이 있을 때, 이 집합의 어떤 원소를 선택하여 합집합을 구하면 원래 집합과 같아지는가?

집합의 부분집합의 합으로 원래 집합을 구하는 문제이다.

예제로 신도시에서 학교르루 배치하는 문제가 나온다.

신도시에 10개의 마을이 만들어진다고 하자.

이 때, 어느 마을에 학교를 세워야 학교의 수를 최소로 하면서 모든 마을이 접근할 수 있는 학교를 세울 수 있을까?

2번, 6번 마을에 학교를 세웠을 때 한 간선으로 모든 노드들이 학교에 갈 수 있음을 확인할 수 있다.

 

이를 변수로 선언하면 다음과 같다.

U={1,2,3,4,5,6,7,8,9,10} //마을(노드) 개수
F={S1,S2,S3,S4,S5,S6,S7,S8,S9,S10} //U의 부분집합으로 구성된 집합 F
S1={1,2,3,8} //S1은 1,2,3,8을 포함하는 부분집합(마을1)
S2={1,2,3,4,8}
S3={1,3,4}
S4={2,3,4,5,7,8}
S5={4,5,6,7}
S6={5,6,7,9,10}
S7={4,5,6,7}
S8={1,2,4,8}
S9={6,9}
S10={6,10}

F의 원소들 중에 어떤 원소들을 선택해야 U와 같아질 수 있는지 생각해 봤을 때 S2US6 = {1,2,3,4,8}U{5,6,7,9,10}일 때 U를 커버할 수 있다.

 

그런데 이를 확인하기 위해서는 F의 원소가 늘어날 수록 시간이 너무 오래 소요된다. (2^n-1) F에서 발견할 수 있는 모든 조합들을 하나씩 합집합 했을 때 U가 되는 조합의 집합 수가 최소인 것을 찾아야 하기 때문이다.

 

그래서 최적해에 근사하는 근사해를 찾는 걸 목표로 한다.

 

알고리즘)

func SetCover
input : U, F={Si}, i=1 ~ n
output : C

1. C = 0
2. while U != 0
3.		U의 원소를 가장 많이 가진 집합 S를 F에서 선택
4.		U = U - Si
5. 		Si를 F에서 제거하고 Si를 C에 추가
6. return C

위의 예시를 예로 들면, 처음 3번 라인을 지날 때 S4이 선택된다.(원소의 개수가 6개로 가장 많기 때문이다.)

U에서 S4를 빼고 F에서 S4를 뺀 다음 C에 추가한다.

U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - {2, 3, 4, 5, 7, 8}
F = {S1 , S2 , S3 , S5 , S6 , S7 , S8 , S9 , S10}

그 다음 S6이 선택된다.

U ={1, 6, 9, 10} - {5, 6, 7, 9, 10}
F = {S1 , S2 , S3 , S5 , S7 , S8 , S9 , S10}

그 다음 S1이 선택된다.

U = {1} - {1, 2, 3, 8}
F = {S2 , S3 , S5 , S7 , S8 , S9 , S10}

결과 C에는 S1,S4,S6이 담겨 있다.

이 알고리즘에서 시간 복잡도를 생각해 보자.

while문은 최악의 경우 F의 모든 원소를 참조해야 한다. 그래서 F의 원소의 개수 (n회)

그리고 while루프 한 번 돌 때, 원소를 가장 많이 포함하고 있는 S를 찾아야 한다. 그렇다면 남아 있는 S들의 수가 최대 n일 때 U와 n번 비교를 하게 되므로, (n^2회)

집합 U에서 집합 S의 원소를 제거하므로 n회

S를 F에서 제거하고 S를 C에 추가하는 것은 1회

 

총 계산하면 n* n^2 = n^3

def set_cover(universe, subsets):
    """Find a family of subsets that covers the universal set"""
    elements = set(e for s in subsets for e in s)
    # Check the subsets cover the universe
    if elements != universe:
        return None
    covered = set()
    cover = []
    # Greedily add the subsets with the most uncovered points
    while covered != elements:
        subset = max(subsets, key=lambda s: len(s - covered))
        cover.append(subset)
        covered |= subset
 
    return cover
 
def main():
    universe = set(range(1, 11))
    subsets = [set([1, 2, 3, 8, 9, 10]),
        set([1, 2, 3, 4, 5]),
        set([4, 5, 7]),
        set([5, 6, 7]),
        set([6, 7, 8, 9, 10])]
    cover = set_cover(universe, subsets)
    print(cover)
 
if __name__ == '__main__':
    main()

6. 작업 스케줄링

 강의실 배정 문제,

강의실은 한정되어 있고 각 강의의 시작 시간과 종료 시간이 있다. 이를 겹치지 않게 배정해야 한다.

빠른 시작 시간을 가진 강의를 배정한다.

알고리즘)

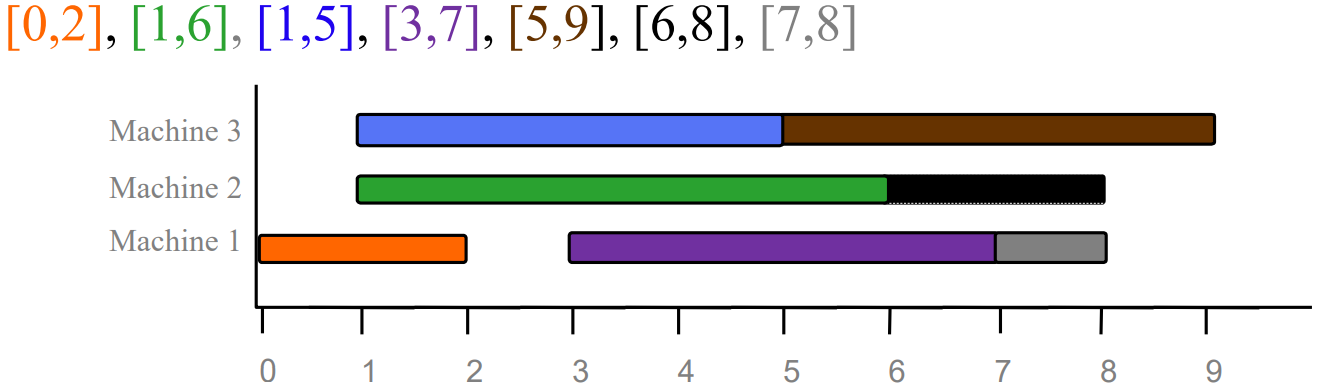
JobScheduling
input : n개의 강의
output : 순서
1. 강의 리스트 : L //시작 시간이 빠른 순으로 정렬되어 있다.
2. while L != 0 
3.		L에서 가장 빠른 시작 시간을 갖는 강의를 가져온다
4. 		if 강의를 수행할 강의실이 있으면
			강의를 배정
6. 		else 새로운 강의실에 강의를 배정
7. 		강의를 L에서 제거
8. return 강의의 순서

강의들은 7개가 있고, 이것의 시작 시간과 끝나는 시간을 담고 있다.

t1=[7,8], t2=[3,7], t3=[1,5], t4=[5,9], t5=[0,2], t6=[6,8], t7=[1,6]

정렬: L = {[0,2], [1,6], [1,5], [3,7], [5,9], [6,8], [7,8]}

 

시간 복잡도에 대해 생각해 본다.

처음 강의 리스트를 정렬하는 데에 nlogn의 시간이 소요된다.

while 문을 지나면서 L에서 강의를 가져다가 강의실을 찾아서 배정해야 하므로 m시간 소요, 이때 m은 배정된 강의실의 수이다.

while 문은 총 n번 수행되므로 m*n 번 반복된다.

 

총 시간 복잡도는 nlogn + mn

def interval_scheduling(stimes, ftimes):
    """Return largest set of mutually compatible activities.
 
    This will return a maximum-set subset of activities (numbered from 0 to n -
    1) that are mutually compatible. Two activities are mutually compatible if
    the start time of one activity is not less then the finish time of the other.
 
    stimes[i] is the start time of activity i.
    ftimes[i] is the finish time of activity i.
    """
    # index = [0, 1, 2, ..., n - 1] for n items
    index = list(range(len(stimes)))
    # sort according to finish times
    index.sort(key=lambda i: ftimes[i])
 
    maximal_set = set()
    prev_finish_time = 0
    for i in index:
        if stimes[i] >= prev_finish_time:
            maximal_set.add(i)
            prev_finish_time = ftimes[i]
 
    return maximal_set
 
 
n = int(input('Enter number of activities: '))
stimes = input('Enter the start time of the {} activities in order: '
              .format(n)).split()
stimes = [int(st) for st in stimes]
ftimes = input('Enter the finish times of the {} activities in order: '
               .format(n)).split()
ftimes = [int(ft) for ft in ftimes]
 
ans = interval_scheduling(stimes, ftimes)
print('A maximum-size subset of activities that are mutually compatible is', ans)